《解析几何》课程大纲
一、课程概况
课程名称 |
解析几何 |
课程代码 |
073BA6004A |
适用专业 |
数学与应用数学 |
开课学期 |
第1学期 |
课程性质 |
学科基础课程 |
学时/学分 |
72/4 |
课程负责人 |
童殷 |
课程组成员 |
罗萍、曾春娜、李体耀 |
预修课程 |
《初等几何》、《初等代数》 |
二、课程目标
课程目标1：掌握向量的基本概念和运算，并会通过向量来建立坐标系；掌握常见的特殊空间曲面、曲线的图形、基本性质，会求其方程、常见的几何量，并会判断一些位置关系。掌握研究二次曲面的一般理论。向量作为一种重要的工具，在后续数学分析、微分几何、普通物理学、复变函数等课程中有广泛的应用，也为高等代数的一些研究提供相应的几何模型与背景；空间曲面、曲线的方程与图形为后续课程中处理图形问题奠定知识基础。
课程目标2：具备统一研究平面解析几何与空间解析几何的能力，提升在较高理论水平的基础上处理中学数学教学中相关问题的能力；培养研究空间图形的直观想象能力、作图能力、抽象思维能力；进一步强化学生的逻辑推理能力与运算能力，提升学习数学的专业能力。
课程目标3：了解解析几何的形成、发展过程，强化将几何问题代数化的基本思想与方法，掌握研究空间图形的特殊方法与一般方法，深入理解数形结合的思想方法，由特殊到一般，具体到抽象的研究方法。丰富学生发现问题、探索问题、解决问题进而获取新知识的思维方法。
课程目标4：了解解析几何与数学其它分支、物理学、工程学的联系，增强学生应用数学的信心；感受几何图形之美，激发学生反思和终身学习数学的热情。
三、课程目标与毕业要求的关系
1、课程目标与毕业要求的对应关系
毕业要求 |
指标点 |
课程目标 |
学会教学 |
学科素养 |
3.2掌握数学学科的基本知识、基本原理和基本技能，理解数学学科知识体系的基本思想和方法，具有良好的数学抽象、逻辑推理、数学建模、直观想象等数学学科专业能力。 |
课程目标1 课程目标2 课程目标3 |
3.3 了解数学与物理和计算机等其他相关学科的联系，了解所教学科与实践应用的联系，掌握一定的数学学科相关知识。 |
课程目标1课程目标4 |
教学能力 |
|
|
学会发展 |
学会反思 |
7.1具有主动学习新知识、掌握新技能的兴趣和意识，具有终身学习和专业发展意识，能通过不断学习和改进养成自主学习的习惯，并能进行职业生涯规划。 |
课程目标1课程目标2 课程目标3 课程目标4 |
沟通合作 |
|
|
2、课程目标与毕业要求的矩阵关系图
名称 |
践行师德 |
学会教学 |
学会育人 |
学会发展 |
师德规范 |
教育情怀 |
学科素养 |
教学能力 |
班级管理 |
综合育人 |
学会反思 |
沟通合作 |
1-1 |
1-2 |
1-3 |
2-1 |
2-2 |
2-3 |
3-1 |
3-2 |
3-3 |
4-1 |
4-2 |
4-3 |
5-1 |
5-2 |
6-1 |
6-2 |
6-3 |
7-1 |
7-2 |
7-3 |
8-1 |
8-2 |
解析几何 |
|
|
|
|
|
|
|
H |
H |
|
|
|
|
|
|
|
|
H |
|
|
|
|
解析几何 |
|
|
H |
|
|
|
M |
|
课程目标1 |
|
|
|
|
|
|
|
H |
H |
|
|
|
|
|
|
|
|
H |
|
|
|
|
课程目标2 |
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
课程目标3 |
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
课程目标4 |
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
H |
|
|
|
|
四、课程教学要求与重难点
序号 |
课程内容框架 |
教学要求 |
教学重点 |
教学难点 |
1 |
向量与坐标 |
知道向量的基本概念，熟练掌握向量的各种运算及其应用；会建立坐标系。了解向量在数学其它分支以及物理学中的应用。 |
线性关系及其应用；数量积、向量积、混合积的概念、性质及其应用；共线、共面向量的各种判别法 |
线性关系的应用；向量积概念的理解和运算；用向量法解决初等几何问题 |
2 |
轨迹与方程 |
会通过建立适当坐标系求解轨迹方程；熟练掌握常见曲线与曲面的参数方程与一般方程；了解空间曲面与曲线的一般方程的形式。 |
常见曲线、曲面的参数方程和一般方程；球坐标系与柱坐标系、坐标间的相互转化、坐标的几何意义；空间曲面与空间曲线的方程的联系与区别 |
理解球坐标系与柱坐标系中坐标的几何意义 |
3 |
平面与空间直线 |
知道点、直线、平面及其之间的相关概念；熟练求解平面、直线的各种方程形式；熟练掌握点、直线、平面间相互位置关系的判定定理与度量关系；了解平面束基本定理的优点及其应用 |
平面、直线的各种方程形式及其求解；点、直线、平面间相互位置关系的判定定理、度量关系 |
利用各种位置关系求解平面、直线方程；异面直线的相关问题；平面束基本定理的证明 |
4 |
柱面、锥面、旋转曲面与二次曲面 |
熟练掌握根据曲面的几何结构求解方程的一般方法、特殊方法；知道常见曲面的标准方程、图形及其简单性质；掌握平行截割法并会利用它研究曲面的图形及其性质 |
柱面、锥面、旋转曲面的定义及求解方程的一般方法；上述三类曲面中的特殊曲面的特殊解法；椭球面、双曲面、抛物面的标准方程、图形及其简单性质 |
方程与曲面间的对应关系；运用平行截割法研究图形及其性质；根据方程作图 |
5 |
二次曲面的一般理论 |
知道二次曲面的相关概念，会判断二次曲面与直线间的位置关系，会求渐近方向、渐近线、渐近曲面、中心、奇点、切线、切平面、径面、奇向、主方向与主径面；了解中心的分类，知道中心、非中心二次曲面与有奇向、没有奇向之间的关系，以及奇向与径面间的关系；掌握直角坐标变换公式，熟练掌握化简二次曲面方程的方法；知道二次曲面的分类；理解统一研究二次曲面的一般方法 |
二次曲面的中心、切平面、主方向、主径面的求解；二次曲面方程的化简 |
构造直角坐标变换化简二次曲面方程 |
五、课程教学内容、教学方式、学时分配及对课程目标的支撑情况
序号 |
课程内容框架 |
教学内容 |
教学方式 |
学时 |
支撑 课程目标 |
1 |
向量与坐标 |
共线、共面向量的概念及几个常用结论，向量的加法、数乘的性质及其在初等几何中的应用 |
讲授、小组合作 |
4 |
课程目标1 课程目标2 课程目标4 |
向量的线性关系与分解及其相关定理的理解；标架与坐标系的概念与分类；坐标与向量线性关系的应用 |
讲授、课堂讨论 |
6 |
课程目标1 课程目标2 |
向量在轴上的射影、数量积、向量积、混合积的概念、性质及其应用 |
讲授、探究、课堂讨论 |
8 |
课程目标1课程目标2 课程目标3 课程目标4 |
2 |
轨迹与方程 |
平面曲线方程的概念，常见平面曲线的方程 |
讲授、课堂讨论 |
1 |
课程目标1 课程目标2 课程目标3 课程目标4 |
空间曲面、空间曲线方程的概念、常见空间曲面、曲线的参数方程与一般方程；球坐标系与柱坐标系，坐标间的相互转化，坐标的几何意义 |
讲授、PPT辅助、课堂讨论 |
5 |
课程目标1 课程目标2 课程目标3 |
3 |
平面与空间直线 |
平面的各种方程形式；平面与点、平面与平面的相关位置的一些定理与应用 |
讲授、探究、课堂讨论 |
6 |
课程目标1课程目标2 课程目标3 |
空间直线的各种方程形式；直线与平面、直线与点、直线与直线的相关位置的一些定理与应用 |
讲授、探究、课堂讨论 |
10 |
课程目标1 课程目标2 课程目标3 |
有轴平面束、平行平面束的基本定理与应用 |
讲授、课堂讨论 |
2 |
课程目标1课程目标2 课程目标3 |
4 |
柱面、锥面、旋转曲面与二次曲面 |
柱面、锥面、旋转曲面的定义及求解方程的一般方法；三类曲面中的特殊曲面的特殊解法；特殊方程与曲面间的对应关系 |
讲授、PPT辅助、课堂讨论 |
6 |
课程目标1课程目标2 课程目标3课程目标4 |
椭球面、双曲面、抛物面的标准方程、图形及其简单性质；学会运用平行截割法研究图形及其性质 |
讲授、探究、PPT辅助、小组合作 |
8 |
课程目标1 课程目标2 课程目标3 课程目标4 |
5 |
二次曲面的一般理论 |
二次曲面的常用符号；二次曲面与直线的相关位置；渐近方向、非渐近方向的定义与判断，渐近线、渐近曲面的方程；中心的定义、分类、求解；切方向、切线、切平面、切点、奇点的定义、求解 |
讲授、课堂讨论 |
6 |
课程目标1 课程目标2 课程目标3课程目标4 |
二次曲面的径面、奇向的定义、求解及其之间的关系，奇向与渐近方向的关系，有无奇向与中心、非中心二次曲面间的关系；二次曲面的主方向、主径面、特征方程、特征根的定义、性质及其求解 |
讲授、探究、课堂讨论 |
6 |
课程目标1 课程目标2 课程目标4 |
右手直角坐标变换分类、公式及其逆变换公式；二次曲面方程的化简与分类 |
讲授、课堂讨论 |
4 |
课程目标1 课程目标2 |
六、课程目标与考核内容
课程目标 |
考核内容 |
课程目标-1：掌握向量的基本概念和运算，并会通过向量来建立坐标系；掌握常见的特殊空间曲面、曲线的图形、基本性质，会求其方程、常见的几何量，并会判断一些位置关系。掌握研究二次曲面的一般理论。向量作为一种重要的工具，在后续课程如微分几何、普通物理学、复变函数等中有广泛的应用，也为高等代数的一些研究提供相应的几何模型与背景；空间曲面、曲线的方程与图形为后续课程中处理图形问题奠定知识基础。 |
向量的线性运算、数量积、向量积、混合积及其应用，平面、直线、球面、柱面、锥面、旋转曲面的方程、常见几何量的求解，位置关系的判断。一般的二次曲面的方程、图形、简单性质。二次曲面与直线的位置关系，二次曲面常见几何量的求解及其之间的关系，二次曲面方程的化简与分类，右手直角坐标变换。 |
课程目标-2：具备统一研究平面解析几何与空间解析几何的能力，提升在较高理论水平的基础上处理中学数学教学中相关问题的能力；培养研究空间图形的直观想象能力、作图能力、抽象思维能力；进一步强化学生的逻辑推理能力与运算能力，提升学习数学的专业能力。 |
向量的各种运算及其应用，常见的特殊曲面、曲线的方程的求解、图形的刻画、常见几何量的关系以及位置关系的判定，二次曲面渐近方向、切线、中心的理解与求解以及二次曲面方程的化简；平时作业 |
课程目标-3：了解解析几何的形成、发展过程，强化将几何问题代数化的基本思想与方法，掌握研究空间图形的特殊方法与一般方法，深入理解数形结合的思想方法，由特殊到一般，具体到抽象的研究方法。丰富学生发现问题、探索问题、解决问题进而获取新知识的思维方法。 |
向量线性关系与分解，标架与坐标，平面、直线相关位置关系的判断，平行截割法；柱面、锥面、旋转曲面方程求解的一般方法以及求解其中特殊曲面的方程的特殊方法，直线与二次曲面的位置关系，二次曲面的渐近方向、渐近线、切线、中心，二次曲面方程的化简，右手直角坐标变换，平时作业 |
课程目标-4：了解解析几何与数学其它分支、物理学、工程学的联系，增强学生应用数学的信心；感受几何图形之美，激发学生反思和终身学习数学的热情。 |
数量积、向量积、混合积的应用，旋转曲面、常见二次曲面、特殊曲线的方程及其图形，二次曲面的渐近线、渐近曲面，平时作业 |
七、考核方式与评价细则
课堂
出勤
10%
评价标准：根据学生上课出勤情况
（1）全勤100分；
（2）旷课一次扣10分；
（3）迟到、早退、事假一次扣5分；
（4）病假、公假、丧假不扣分；
（5）旷课三次以上不及格。
平时
作业
10%
评价标准：根据学生提交的作业情况
每个班分成三至四个小组，每次批改一个小组的作业，根据学生作业完成情况给出A+(全对且字迹工整)、A(全对)、B(错一个)、C(错两个及以上)四个等级，一学期一个学生大约上交四次作业。
（1）全部为A+计100分；
（2）两次及以上A+，95分；
（3）一次及以上A+，90分；
（4）一次及以上A，85分；
（5）其他80分；
在此标准下，少交一次作业扣10分。
平时
测验
30%
评价标准：三次单元检测成绩，每次占百分之十。严格按照《解析几何》平时测验试题参考答案及评分细则进行阅卷。
期末
考试
50%
评价标准：严格按照《解析几何》期末试题参考答案及评分细则进行阅卷。
综合
成绩
100%
课堂出勤（10%）+平时作业（10%）+平时测验（30%）+期末考试（50%）
八、课程目标达成度评价
1、课程目标达成度评价机制
（1）评价机构
课程目标达成度评价在best365体育官网登录入口教学指导委员会的指导下进行，由课程负责人负责实施，承担该门课程的所有任课教师共同参与评价。
（2）数据来源
课程目标达成度评价采用的数据源自课程考核的成绩，课程考核成绩包含出勤成绩、课堂表现成绩、平时作业成绩、期中测试成绩（期中论文成绩或报告成绩）和期末试卷考核成绩等。
（3）评价周期
本专业课程目标达成度评价周期一般为1年。
2、课程目标达成评价方法
每门课程应有3-5个课程目标，每个课程目标对8个毕业要求分解指标点的支撑情况是不相同的，按照各个课程目标对8个毕业要求分解指标点的支撑力度，对每个课程目标赋予权重值。根据一门课程的所有课程目标都应该对该课程的整体目标达成有所贡献的原则，该课程的整体目标达成度由该课程的所有课程目标达成度的加权平均值确定。
（1）各个课程目标权重值的确定
每门课程一般有3-5个课程目标，每个课程目标对8个毕业要求的支撑力度有高（H）、中（M）、低（L）之分，为了便于操作，赋值H=3, M=2, L=1。假设某门课程有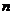
个课程目标，第
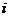个课程目标对8个毕业要求分解指标点的支撑力度有
个H、
个M和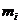
个L，那么，第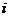个课程目标的分值
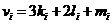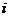，第个课程目标的权重值确定为
，
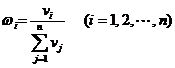所有课程目标的权重值之和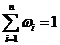
。
（2）各个课程目标达成度的计算
各个课程目标达成度评价采用“考核成绩分析法”，随机抽取1-2个教学班级为样本，课程考核材料包括考试、测验、作业、考勤、实验（实习、设计）报告、读书报告等。每个课程目标都有支撑该课程目标的教学内容，假设某门课程有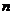个课程目标，支撑第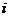个课程目标的教学内容试卷考核总分为
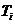，抽取的样本学生该部分的试卷考核平均分数为
，
是该课程支撑第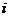个课程目标的形成性考核的平均得分（形成性考核一般包括课堂表现、平时作业和平时测验等），支撑第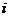个课程目标的形成性考核总分为
，
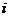是期末试卷考核占总考核的比例，那么，第个课程目标的达成度计算公式为
，
若某个
，即期末考核试卷中无支撑该课程目标的内容，则
。
（3）课程的整体目标达成度的确定
一门课程的整体目标达成度由该课程的所有课程目标达成度的加权平均值确定。假设某门课程有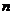个课程目标，第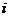个课程目标的权重值为
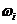，第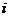个课程目标的达成度为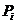
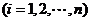，那么，该门课程的整体目标达成度为
.
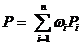（4）课程的整体目标达成度评价标准
参照best365体育官网登录入口学分制管理办法及学士学位授予条例，平均学分绩点≥2.0者才可获得理学学士学位。由于学分绩点2.0对应课程考核成绩为70分，因此，本专业课程的整体目标达成度评价标准设定为“达到0.70为评价合格”。
九、本课程各个课程目标的权重
依据第八部分中的课程目标达成度评价方法，计算得到本课程的各个课程目标的权重如下：
课程目标 |
课程目标-1 |
课程目标-2 |
课程目标-3 |
课程目标-4 |
权值 |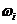
0.346 |
0.231 |
0.192 |
0.231 |
十、持续改进
根据学生的课堂表现、平时作业、平时测验情况及教学督导的反馈，检验学生对本课程涉及的学科素养和学会反思的达成情况，及时对教学中的不足之处进行改进，调整教学指导策略；根据学生的课堂表现、平时作业、平时测验及期末考试成绩，检验本课程所支撑的毕业要求分解指标点的达成度情况；根据本课程所支撑的毕业要求分解指标点的达成度情况，参考优秀专业经验，在本学院教学指导委员会指导下，重新修订本课程大纲，实现持续改进。
十一、推荐教材及参考书目
1.推荐教材
吕林根，许子道. 解析几何（第四版）.北京：高等教育出版社，2006.
丘维声. 解析几何.上海：复旦大学出版社，2014.
杨文茂、李全英. 空间解析几何. 武汉：武汉大学出版社，2004.
2.参考书目
吕林根.解析几何学习辅导书.北京：高等教育出版社，2006.
蒋大为，宋伟杰.解析几何导教导学导考.西安：西北工业大学出版社，2007
吕杰，陈奇斌等.解析几何.北京：科学出版社，2017.
