《高等代数I-II》课程大纲
一、课程概况
课程名称 |
高等代数I-II |
课程代码 |
073BA8003A、073BAA003A |
适用专业 |
数学与应用数学 |
开课学期 |
第1、2学期 |
课程性质 |
学科基础课程 |
学时/学分 |
216/10 |
课程负责人 |
汪定国 |
课程组成员 |
张新功、李庆、俞晓燕、蔡钢、钱文华 |
预修课程 |
中学数学 |
二、课程目标
课程目标1:掌握多项式理论、线性代数理论中的基本概念、基础知识与基本理论,从而提升学生的专业知识素质,为后续课程及其它相关学科的学习建立良好的知识储备。
课程目标2:理解基本定理的证明过程,训练学生的抽象思维、逻辑推理和代数运算的能力,培养学生解决问题的基本意识与技能,提高学生的专业能力素质,为后续专业课程、其它相关学科的学习以及自主学习与职后发展奠定坚实的能力基础。
课程目标3:使学生进一步掌握具体与抽象、特殊与一般、有限与无限等辩证关系,培养其辩证唯物主义观点,提高学生的直观想象以及数学建模的能力,掌握本课程所涉及的现代数学中的重要思想方法,为后续专业课程、其它相关学科的学习以及自主学习与职后发展奠定坚实的思想方法基础。
课程目标4:使学生对中学数学有关内容从理论上有更深刻的认识,培养学生的终身学习和专业发展意识,以便能够高屋建瓴地掌握和处理中学数学教材;同时,通过课前预习、课堂引导和启发、课后作业等方式,激发学生探索与求知的欲望,培养学生自主学习与职后发展的能力。
三、课程目标与毕业要求的关系
1、课程目标与毕业要求的对应关系
毕业要求 |
指标点 |
课程目标 |
学会教学 |
学科素养 |
3.2掌握数学学科的基本知识、基本原理和基本技能,理解数学学科知识体系的基本思想和方法,具有良好的数学抽象、逻辑推理、数学建模、直观想象等数学学科专业能力。 |
课程目标1 课程目标2 课程目标3 |
3.3了解数学与物理和计算机等其他相关学科的联系,了解所教学科与实践应用的联系,掌握一定的数学学科相关知识。 |
课程目标1 课程目标2 课程目标3 |
教学能力 |
|
|
学会发展 |
学会反思 |
7.1具有主动学习新知识、掌握新技能的兴趣和意识,具有终身学习和专业发展意识,能通过不断学习和改进养成自主学习的习惯,并能进行职业生涯规划。 |
课程目标1 课程目标2 课程目标3 课程目标4 |
沟通合作 |
|
|
2、课程目标与毕业要求的矩阵关系图
名称 |
践行师德 |
学会教学 |
学会育人 |
学会发展 |
师德规范 |
教育情怀 |
学科素养 |
教学能力 |
班级管理 |
综合育人 |
学会反思 |
沟通合作 |
1-1 |
1-2 |
1-3 |
2-1 |
2-2 |
2-3 |
3-1 |
3-2 |
3-3 |
4-1 |
4-2 |
4-3 |
5-1 |
5-2 |
6-1 |
6-2 |
6-3 |
7-1 |
7-2 |
7-3 |
8-1 |
8-2 |
高等代数I-II |
|
|
|
|
|
|
|
H |
H |
|
|
|
|
|
|
|
|
H |
|
|
|
|
高等代数I-II |
|
|
H |
|
|
|
M |
|
课程目标1 |
|
|
|
|
|
|
|
H |
H |
|
|
|
|
|
|
|
|
M |
|
|
|
|
课程目标2 |
|
|
|
|
|
|
|
H |
H |
|
|
|
|
|
|
|
|
H |
|
|
|
|
课程目标3 |
|
|
|
|
|
|
|
H |
H |
|
|
|
|
|
|
|
|
H |
|
|
|
|
课程目标4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
四、课程教学要求与重难点
序号 |
课程内容框架 |
教学要求 |
教学重点 |
教学难点 |
1 |
多项式 |
(1)掌握数域的概念,能够判定一些数集是否数域,了解任何数域都包含有理数域。 (2)掌握数域P上一元多项式的概念、运算及多项式的和与积的次数,会用多项式相等求待定系数。 (3)掌握带余除法定理,能熟练地用竖式作带余除法;掌握多项式整除的概念和性质,能熟练地运用这些性质;能熟练地运用综合除法。 (4)掌握最大公因式的概念,特别是 ;掌握best365体育官网登录入口关于最大公因式的存在性、基本关系式的结论,理解其证明;能熟练地运用辗转相除法求最大公因式;掌握多项式互素的概念、多项式互素的条件及多项式互素的性质的证明和结论,并能熟练地运用它们。 ;掌握best365体育官网登录入口关于最大公因式的存在性、基本关系式的结论,理解其证明;能熟练地运用辗转相除法求最大公因式;掌握多项式互素的概念、多项式互素的条件及多项式互素的性质的证明和结论,并能熟练地运用它们。 (5)掌握不可约多项式概念,不可约多项式与任意多项式的关系及不可约多项式性质的证明及结论,并能正确地运用它们;掌握因式分解及唯一性定理的结论和标准分解式,会用标准分解式求最大公因式。 (6)理解多项式的导数及重因式的概念,掌握多项式有无重因式的判别法则。 (7)掌握多项式函数及多项式根的概念;掌握余数定理、因式定理及根的最多个数的结论及证明,并能正确运用它们。了解数域P上多项式相等与多项式函数相等(即恒等)的一致性。 (8)掌握代数基本定理的结论,复数域上多项式因式分解的结论;了解实系数多项式非实复根的性质;掌握实数域上多项式因式分解的结论。 (9)理解有理系数多项式的因式分解问题可以归结为整系数多项式的因式分解问题,进而熟练地掌握有理系数多项式有理根的求法;掌握艾森斯坦因判别法判定整系数多项式在有理数域上不可约,同时明确有理数域上存在任意次数的不可约多项式。 |
多项式互素、不可约多项式、本原多项式的概念和性质、最大公因式和有理系数多项式有理根的求法。 |
因式分解定理的应用。 |
2 |
行列式 |
(1)明确什么是奇、偶排列及其在对换之下的性质。 (2)正确理解n级行列式的定义。 (3)掌握行列式的性质,能够准确、熟练地运用这些性质,并学会计算行列式的一些常用方法。 (4)掌握克兰姆法则:明确定理的前提、结论,熟记求解公式;明确n个方程的n元齐次线性方程组只有零解的条件。 |
行列式的性质、计算。 |
字母行列式的计算。 |
3 |
线性方程组 |
(1)理解线性方程组的同解和初等变换的概念;明确消元法的理论根据;理解消元法与矩阵初等行变换的关系;能熟练地运用矩阵的初等行变换解一般线性方程组。 (2)理解n维向量和数域P上n维向量的概念;掌握n维向量的加法、数量乘法及其运算性质。 (3)理解向量的线性组合及向量组等价概念;正确理解和掌握向量组的线性相关、线性无关概念并熟练掌握它们的判别方法;熟练掌握向量组的极大无关组和秩的概念及求法。 (4)理解和掌握矩阵的秩的概念,能熟练地求矩阵的秩。 (5)掌握线性方程组有解判别定理及其应用。 (6)明确齐次线性方程组的解集合的基本性质,熟练掌握齐次线性方程组的基础解系的概念、求法,熟练掌握一般线性方程组的解的结构。 |
消元法、向量组的线性相关、线性无关、向量组与矩阵的秩、线性方程组的有解判别定理、齐次线性方程组的基础解系。 |
向量组的线性相关性的判定。 |
4 |
矩阵 |
(1)明确矩阵和矩阵相等的概念。 (2)掌握矩阵的加法、数量乘法、乘法、转置及其运算性质,并能熟练地运用它们。 (3)掌握矩阵乘积的行列式及秩的定理。 (4)正确理解和掌握可逆矩阵的概念;掌握可逆矩阵的性质,矩阵可逆的充要条件和求逆矩阵的方法。 (5)理解初等矩阵的概念;掌握初等矩阵与初等变换的关系;理解用初等变换求逆矩阵的原理,并且能熟练地使用这个方法;理解矩阵等价的概念,掌握矩阵的等价标准形定理。 (6)理解分块矩阵的含义;理解分块矩阵的加法、乘法的意义,会用分块矩阵去简化运算和证明有关问题。 |
矩阵的运算,特别是矩阵乘法、矩阵可逆的条件及逆矩阵的计算。 |
分块矩阵的意义及运算、初等矩阵、用初等变换的方法求逆矩阵、分块矩阵的逆。 |
5 |
二次型 |
(1)理解二次型、线性替换的概念。 (2)掌握二次型(对称矩阵)的标准形及化简二次型(对称矩阵)的理论推导。 (3)掌握复系数二次型的规范形的唯一性、惯性定理及理论推导。 (4)理解并能熟练应用(半)正定二次型(矩阵)的定义、性质及判定,总结出矩阵的合同不变性质;能够熟练应用非退化线性替换及矩阵的合同变换化简二次型、对称矩阵成标准形或规范形,应用二次型(对称矩阵)的有关理论于某些等式或不等式的证明。 |
矩阵的合同关系;二次型化标准形,惯性定理,矩阵正定,半正定性的判定。 |
复数域和实数域上二次型的规范形的唯一性、惯性定理、正定二次型的判别条件。 |
6 |
线性空间 |
(1)正确理解集合的概念,明确集合的相等、子集、空集等概念;掌握集合的简单运算及其性质;掌握证明两个集合相等的最基本的方法;正确理解和掌握映射、变换、映上的映射、1-1的映射、1-1对应、映射的相等、映射的乘积、逆映射等概念。 (2)掌握线性空间的概念及其简单性质,初步了解公理化的思想方法;了解常用的线性空间。 (3)掌握n维线性空间的维数与基的概念及其求法;理解基在线性空间理论中所起的重要作用。 (4)掌握向量空间中向量坐标的概念及其意义、基变换及坐标变换公式、过渡矩阵的概念及其性质。 (5)理解和掌握线性空间的子空间的概念和判别方法;理解有限个向量生成的子空间的概念,会求它的一组基;掌握基的扩充定理。 (6)掌握子空间的交与和概念;掌握维数公式。 (7)正确理解子空间的和是直和的概念;掌握子空间的和是直和的充要条件;理解任一n维线性空间都能分解成两个子空间的直和。 (8)理解线性空间同构的概念、性质及其重要意义;掌握有限维线性空间同构的充要条件。 |
线性空间的维数与基、子空间的和、直和、维数公式、线性空间的同构。 |
线性空间的定义;子空间的直和、线性空间同构的定义、性质及两个有限维线性空间同构的充要条件。 |
7 |
线性变换 |
(1)理解线性变换的定义,会判别一个变换是不是线性变换;掌握线性变换的简单性质。 (2)掌握线性变换的加法、数量乘法、乘法及其简单性质;理解和掌握可逆线性变换的概念。 (3)理解线性变换的多项式;正确理解线性变换的矩阵的概念,并能熟练地求出线性变换在给定基下的矩阵;掌握矩阵相似的概念及其基本性质;牢固掌握以下三个基本关系:1) 取定数域P上n维线性空间V的一组基后,V上全体线性变换的集合L(V)与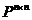 间存在同构映射;2)线性变换前后,向量坐标间的关系;3) 基变换前后,线性变换矩阵间的关系。 间存在同构映射;2)线性变换前后,向量坐标间的关系;3) 基变换前后,线性变换矩阵间的关系。 (4)理解特征值和特征向量的概念并且熟练地掌握其求法;理解特征子空间、特征多项式的概念,明确特征多项式的基本性质; (5)全面掌握线性变换(矩阵)可以对角化的条件及化简方法。 (6)掌握线性变换的值域、核、秩、零度等概念;深刻理解和掌握线性变换的值域与它对应的矩阵的秩的关系及线性变换的秩和零度间的关系。 (7)掌握不变子空间的定义;会判定一个子空间是否是σ-子空间;深刻理解不变子空间与线性变换矩阵化简之间的关系;掌握将空间V按特征值分解成不变子空间的直和表达式。 |
线性变换的矩阵、特征值、特征向量的定义、性质与计算、矩阵相似的定义与性质;线性变换(矩阵)可以对角化的判定及其化法。 |
哈密尔顿-凯莱定理、线性变换在某一组基下的矩阵为对角阵的充要条件、线性变换的值域、核、秩、零度、线性变换的值域与它对应的矩阵的秩的关系及线性变换的秩和零度间的关系、不变子空间。 |
8 |
欧几里得空间 |
(1)正确理解内积概念;掌握欧氏空间、向量的长度、两个向量的夹角、正交、距离等概念;掌握柯西—布涅柯夫斯基不等式和三角不等式;牢固掌握度量矩阵的概念以及不同基的度量矩阵的关系。 (2)掌握标准正交基的概念,能熟练地求出一组标准正交基并且理解标准正交基的作用;掌握正交矩阵的概念、性质及其与标准正交基的关系。 (3)理解欧氏空间同构的概念及欧氏空间同构的充要条件。 (4)理解和掌握正交变换的概念和性质,明确正交变换与正交矩阵的关系。 (5)正确理解和掌握两个子空间正交的概念,掌握正交与直和的关系,及欧氏空间中的每一个子空间都有唯一的正交补的性质。 (6)深刻理解并掌握任一个对称矩阵均可正交相似于一个对角阵,并掌握求正交阵的方法。能用正交变换化实二次型为标准形。 |
欧氏空间的定义及性质、向量的长度,两个向量的夹角、正交及度量矩阵等概念和基本性质、正交向量组、标准正交基的概念、施密特正交化、欧氏空间同构的意义及同构与空间维数之间的关系、正交变换的概念及几个等价关系、正交变换与向量的长度,标准正交基,正交矩阵间的关系、两个子空间正交的概念、正交与直和的关系、正交矩阵、用正交变换化实二次型为标准形。 |
正交变换的概念及几个等价关系、正交变换与向量的长度、标准正交基、正交矩阵间的关系、对称变换的概念及其性质、对称变换与实对称矩阵之间的关系。 |
五、课程教学内容、教学方式、学时分配及对课程目标的支撑情况
序号 |
课程内容框架 |
教学内容 |
教学方式 |
学时 |
支撑 课程目标 |
1 |
多项式 |
数域:定义、例子及相关结论。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 课程目标4 |
一元多项式的定义和运算:一元多项式的基本概念及一元多项式的运算与性质。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标3 课程目标4 |
多项式的整除性:带余除法定理、整除的定义和基本性质、综合除法。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 课程目标4 |
多项式的最大公因式:最大公因式的概念、性质、辗转相除法和互素多项式。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标4 |
多项式的因式分解定理:不可约多项式的概念及性质、因式分解定理。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 课程目标4 |
多项式的重因式:多项式的导数、多项式的重因式的概念及多项式有重因式的充要条件。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 |
多项式函数:多项式函数和多项式的根的概念、余数定理、因式定理、多项式根的个数定理、多项式相等的条件。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 课程目标2 课程目标3 课程目标4 |
复数域和实数域上多项式的因式分解:复数域上一元多项式的因式分解定理与实数域上因式分解定理。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 课程目标3 课程目标4 |
有理数域上多项式的可约性及有理根:本原多项式、高斯引理、整系数多项式在有理数域上的可约性问题、有理数域上多项式的有理根、艾森斯坦因判别法、有理数域上存在任意次数的不可约多项式。 |
讲授、课堂讨论、课后练习 |
8 |
课程目标1 课程目标2 课程目标3 课程目标4 |
2 |
行列式 |
排列:排列的概念:逆序数及排列的奇偶性的概念、对换及其对排列的作用。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 |
n级行列式的定义:二级和三级行列式的结构、n级行列式的定义。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 课程目标3 |
n级行列式的性质:可转性、可提性、可分性、行列式为0的充分条件、可消性、可换性。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标3 |
行列式按一行(列)展开:子式与代数余子式的概念;行列式按一行(列)展开 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标3 |
行列式的计算:行列式计算方法介绍及举例。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 课程目标3 |
克兰姆法则:克兰姆法则及应用。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 课程目标2 课程目标4 |
3 |
线性方程组 |
消元法:线性方程组的消元法,矩阵的概念,矩阵的初等变换的概念,线性方程组的同解变换与矩阵的初等行变换,任何一个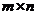 矩阵经初等行变换化为阶梯形矩阵定理,用矩阵的行初等变换解线性方程组。 矩阵经初等行变换化为阶梯形矩阵定理,用矩阵的行初等变换解线性方程组。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标3 |
n维向量空间:n维向量的定义、运算及性质。 |
讲授、课堂讨论 |
2 |
课程目标1 |
线性相关性:线性组合、等价向量组等定义及性质、线性相关、线性无关的定义及性质、向量组的基本性质定理、极大无关组、秩的定义及性质。 |
讲授、课堂讨论、课后练习 |
8 |
课程目标1 课程目标2 课程目标3 课程目标4 |
矩阵的秩:行秩、列秩与矩阵的秩、方阵非退化与满秩的关系、k级子式的定义、矩阵的秩即非零子式的最大级数、初等变换不改变矩阵的秩的定理、用初等变换法求矩阵的秩。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 课程目标3 |
线性方程组有解判别法:线性方程组有解判别定理及解的个数定理、线性方程组解的行列式结构公式。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 课程目标3 |
线性方程组解的结构:齐次线性方程组的解集合对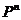 的两个运算的封闭性、齐次线性方程组的基础解系的概念、求法以及齐次线性方程组解的结构、非齐次线性方程组解的结构。 的两个运算的封闭性、齐次线性方程组的基础解系的概念、求法以及齐次线性方程组解的结构、非齐次线性方程组解的结构。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 课程目标3 课程目标4 |
4 |
矩阵 |
矩阵的概念:矩阵产生的背景、矩阵的定义、矩阵相等的定义。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 |
矩阵的运算:矩阵的加法、数量乘法、乘法和转置等运算的定义及相应的性质。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 |
矩阵乘积的行列式与秩:矩阵的乘积的行列式的计算方法及理论保证、矩阵乘积的秩的界。 |
讲授、课堂讨论 |
4 |
课程目标1 课程目标2 课程目标3 |
矩阵的逆:可逆矩阵及逆矩阵的概念、可逆矩阵的性质、求逆矩阵的公式。 |
讲授、课堂讨论 |
4 |
课程目标1 课程目标3 |
矩阵的分块:分块矩阵、分块矩阵的运算、准对角矩阵。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 课程目标3 |
初等矩阵:初等矩阵的定义及基本性质、矩阵等价的概念及等价标准形、用初等变换求逆矩阵的原理及方法。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 课程目标3 |
5 |
二次型 |
二次型及其矩阵表示: 二次型的定义及其矩阵表示、线性替换的定义及其矩阵表示、线性替换前后二次型矩阵之间的关系、合同的定义及其性质。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标3 |
标准形:二次型的基本定理、用矩阵的合同变换求标准形、用矩阵的初等变换求标准形。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 |
唯一性:二次型的秩的定义、复数域上二次型的规范形、实数域上二次型的规范形及惯性定理。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 |
正定二次型:正定二次型及其判定、正定矩阵及其性质、半正定矩阵及其等价条件。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 |
6 |
线性空间 |
集合与映射:集、子集、集合的相等、集合的交与并及其运算规律、映射、变换、映上的映射、1-1的映射、1-1对应、映射的相等、映射的乘积、可逆映射。 |
讲授、PPT辅助、课堂讨论、课后练习 |
3 |
课程目标1 课程目标4 |
线性空间的定义与简单性质:线性空间的定义及例子、线性空间的简单性质。 |
讲授、课堂讨论、课后练习 |
3 |
课程目标1 课程目标4 |
维数、基与坐标:线性空间中向量组的线性相关性、线性空间的维数、基与坐标以及具体例子。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标3 课程目标4 |
基变换与坐标变换:过渡矩阵的定义及性质、基变换、同一向量在不同基下的坐标之间的关系,即坐标变换公式。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 课程目标3 |
线性子空间:子空间的定义及判别法、生成子空间定义及性质、子空间的基与全空间的基的关系。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标3 |
子空间的交与和:子空间的交与和的定义及性质、维数公式。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 课程目标3 |
子空间的直和:子空间的和是直和的定义、和是直和的三个充要条件、n维线性空间分解成两个子空间的直和的方法。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 课程目标3 |
线性空间的同构:同构映射的概念、同构映射的性质以及同构的充要条件。 |
讲授、课堂讨论 |
4 |
课程目标1 课程目标2 |
7 |
线性变换 |
线性变换的定义:线性变换的基本概念、线性变换的简单性质。 |
讲授、课堂讨论、课后练习 |
2 |
课程目标1 课程目标4 |
线性变换的运算:线性变换的加法、数量乘法、乘法、逆变换、方幂及多项式等的定义及性质。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标3 |
线性变换的矩阵:线性变换的矩阵的定义、线性变换与矩阵的同构对应、向量的像的坐标公式、基变换前后线性变换矩阵间的关系、矩阵的相似及其基本性质。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标2 课程目标3 |
特征值与特征向量:特征值、特征向量和特征子空间的定义和求法、特征多项式的定义及其基本性质。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 课程目标3 |
可对角化的矩阵:属于不同特征值的特征向量的线性无关性、特征子空间的维数与所属特征值的重数的关系、线性变换和矩阵可对角化的条件。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 课程目标3 |
线性变换的值域与核:线性变换的值域与核的概念与性质、线性变换的秩与零度及它们间的关系。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 课程目标3 |
不变子空间:不变子空间的概念及判别法、不变子空间的性质。 |
讲授、课堂讨论、课后练习 |
4 |
课程目标1 |
8 |
欧几里得空间 |
欧氏空间的定义与基本性质:欧氏空间的定义与内积的简单性质、向量的长度及其性质(包括柯西—布涅柯夫斯基不等式,三角不等式)、两向量的夹角与正交、“勾股定理”、基的度量矩阵和内积的矩阵表示。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 |
标准正交基:标准正交基的定义、存在性、作用及求法(施密特正交化方法)、正交矩阵的定义、性质及其与标准正交基的关系。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 课程目标3 |
欧氏空间的同构:定义及充要条件。 |
讲授、课堂讨论 |
3 |
课程目标1 课程目标2 |
正交变换:正交变换的定义、性质;n维欧氏空间的正交变换与n级正交矩阵的关系。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 |
欧氏空间的子空间:子空间的正交关系、子空间的正交补。 |
讲授、课堂讨论、课后练习 |
3 |
课程目标1 课程目标3 |
实对称矩阵的标准形:实对称矩阵的性质与对称变换、实对称矩阵的标准形。 |
讲授、课堂讨论、课后练习 |
6 |
课程目标1 课程目标2 课程目标3 |
六、课程目标与考核内容
课程目标 |
考核内容 |
课程目标1:掌握多项式理论、线性代数理论中的基本概念、基础知识与基本理论,从而提升学生的专业知识素质,为后续课程及其它相关学科的学习建立良好的知识储备。 |
多项式的运算及性质、多项式的整除概念及基本性质、最大公因式的概念、多项式互素的定义及性质、不可约多项式的概念及性质、重因式的概念及判别方法、有理系数多项式的有理根的求法、n级行列式的定义及性质、消元法与矩阵的初等行变换解一般线性方程组的方法、n维向量的运算及性质、向量组的线性相关性的有关概念及判定方法、矩阵的秩的求法、矩阵的运算及性质、矩阵的可逆及逆矩阵的相关概念及性质、初等矩阵的定义及用初等变换求可逆矩阵的逆矩阵的方法、二次型的标准形的求法、正定二次型的定义、性质及判定方法、线性空间的定义、性质与判别方法、维数、基与坐标的定义及求法、基变换与坐标变换公式、线性子空间的定义及性质、子空间的交与和的定义、性质及求法、子空间的直和的定义、性质及判别、线性空间同构的定义及同构映射的性质、线性变换的定义、性质及判别方法、线性变换运算及性质、矩阵相似的定义、线性变换与矩阵的特征值与特征向量的定义、性质及求法、线性变换的值域与核的定义、性质及求法、不变子空间的定义与性质、欧氏空间的定义、性质及判别方法、向量的度量性质、标准正交基的定义、正交矩阵的定义、欧氏空间同构的定义、欧氏空间的子空间的定义及性质,同时包含出勤、课堂表现和平时作业的完成情况以及平时测验成绩。 |
课程目标2:理解基本定理的证明过程,训练学生的抽象思维、逻辑推理和代数运算的能力,培养学生解决问题的基本意识与技能,提高学生的专业能力素质,为后续专业课程、其它相关学科的学习以及自主学习与职后发展奠定坚实的能力基础。 |
带余除法定理、最大公因式存在定理、互素的充要条件、因式分解及唯一性定理、余数定理、因式定理及根的个数定理、复系数与实系数多项式的因式分解定理、有理系数多项式的因式分解的有关定理、艾森斯坦判别法、行列式的计算、克兰姆法则、有关向量组的性质的基本定理、矩阵的秩的有关定理、线性方程组的有解判定定理、线性方程组的解的结构定理、矩阵乘积的行列式与秩、初等矩阵的作用、二次型的基本定理、惯性定理、线性空间中基的扩充定理、维数公式、两个线性空间同构的充要条件、线性变换与矩阵之间的对应关系、哈密尔顿-凯莱定理、线性变换的矩阵是对角阵的判定条件、线性变换的秩与零度之间的关系、标准正交基的定义、存在性、作用及求法(施密特正交化方法)、正交矩阵与标准正交基的关系、欧氏空间同构的充要条件、正交变换与正交矩阵的关系、实对称矩阵的标准形。同时包含出勤、课堂表现和平时作业的完成情况以及平时测验成绩。 |
课程目标3:使学生进一步掌握具体与抽象、特殊与一般、有限与无限等辩证关系,培养其辩证唯物主义观点,提高学生的直观想象以及数学建模的能力,掌握本课程所涉及的现代数学中的重要思想方法,为后续专业课程、其它相关学科的学习以及自主学习与职后发展奠定坚实的思想基础。 |
一元多项式定义的理解、多项式函数的本质的理解、综合除法的应用、余数定理、因式定理及根的个数定理的应用、复系数与实系数多项式的因式分解定理的应用、艾森判别法的应用、有理系数多项式有理根的求法、行列式定义及性质的应用、行列式的计算方法、用矩阵的初等行变换解一般的线性方程组、向量组的线性相关性的判定方法、矩阵的秩的求法、线性方程组的解的结构定理的应用、矩阵乘积的行列式与秩的定理的应用、逆矩阵的求法、分块矩阵的应用、二次型的标准形的求法、线性空间的基、维数及坐标的求法、基变换与坐标变换公式的应用、子空间的判别方法、基扩充定理的应用、维数公式的应用、线性空间的交与和的求法、直和的判定方法、线性变换的运算、矩阵相似性质的应用、线性变换的矩阵可对角化的判别方法、线性变换的值域与核的求法、欧氏空间的标准正交基的求法、欧氏空间的子空间的正交补的求法、实对称矩阵的标准形的求法。同时包含出勤、课堂表现和平时作业的完成情况以及平时测验成绩。 |
课程目标4:使学生对中学数学有关内容从理论上有更深刻的认识,培养学生的终身学习和专业发展意识,以便能够高屋建瓴地掌握和处理中学数学教材;同时,通过课前预习、课堂引导和启发、课后作业等方式,激发学生探索与求知的欲望,培养学生自主学习与职后发展的能力。 |
数域的判定、一元多项式的定义、多项式的整除与带余除法定理、多项式的最大公因式、多项式的因式分解、多项式的根的定义、克兰姆法则的应用、向量的线性相关性、线性方程组的求解、消元法的理论依据、集合与映射的定义与性质、线性空间的定义、线性变换的定义的理解。同时包含出勤、课堂表现和平时作业的完成情况以及平时测验成绩。 |
七、考核方式与评价细则
课堂
出勤
10%
评价标准:根据学生上课出勤情况
(1)全勤100分;
(2)旷课一次扣10分;
(3)迟到、早退、事假一次扣5分;
(4)上课时玩手机一次扣5分;
(5)上课睡觉一次扣5分;
(6)病假、公假、丧假不扣分;
(7)旷课三次以上不及格。
平时
作业
10%
评价标准:一个教学班分成三至四个小组,每次批改一个小组的作业,根据学生作业完成程度给出A+、A-、B+、B-、C五个等级,一学期一个学生至少上交五次作业。在所交作业的所有次数中,取等级最高的五次评定分数:
(1)一个A+计20分;
(2)一个A-计18分;
(3)一个B+计16分;
(4)一个B-计14分;
(5)一个C计12分。
平时
测验
30%
评价标准:三次单元检测成绩,每次占百分之十。严格按照《高等代数I-II》平时测验试题参考答案及评分细则进行阅卷。
期末
考试
50%
评价标准:严格按照《高等代数I-II》期末试题参考答案及评分细则进行阅卷。
综合
成绩
100%
课堂出勤(10%)+平时作业(10%)+平时测验(30%)+期末考试(50%)
八、课程目标达成度评价
1、课程目标达成度评价机制
(1)评价机构
课程目标达成度评价在best365体育官网登录入口教学指导委员会的指导下进行,由课程负责人负责实施,承担该门课程的所有任课教师共同参与评价。
(2)数据来源
课程目标达成度评价采用的数据源自课程考核的成绩,课程考核成绩包含出勤成绩、课堂表现成绩、平时作业成绩、期中测试成绩(期中论文成绩或报告成绩)和期末试卷考核成绩等。
(3)评价周期
本专业课程目标达成度评价周期一般为1年。
2、课程目标达成评价方法
每门课程应有3-5个课程目标,每个课程目标对8个毕业要求分解指标点的支撑情况是不相同的,按照各个课程目标对8个毕业要求分解指标点的支撑力度,对每个课程目标赋予权重值。根据一门课程的所有课程目标都应该对该课程的整体目标达成有所贡献的原则,该课程的整体目标达成度由该课程的所有课程目标达成度的加权平均值确定。
(1)各个课程目标权重值的确定
每门课程一般有3-5个课程目标,每个课程目标对8个毕业要求的支撑力度有高(H)、中(M)、低(L)之分,为了便于操作,赋值H=3, M=2, L=1。假设某门课程有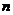 个课程目标,第
个课程目标,第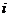 个课程目标对8个毕业要求分解指标点的支撑力度有
个课程目标对8个毕业要求分解指标点的支撑力度有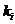 个H、
个H、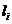 个M和
个M和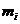 个L,那么,第
个L,那么,第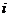 个课程目标的分值
个课程目标的分值 ,第
,第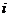 个课程目标的权重值确定为
个课程目标的权重值确定为
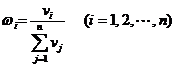 ,
,
所有课程目标的权重值之和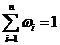 。
。
(2)各个课程目标达成度的计算
各个课程目标达成度评价采用“考核成绩分析法”,随机抽取1-2个教学班级为样本,课程考核材料包括考试、测验、作业、考勤、实验(实习、设计)报告、读书报告等。每个课程目标都有支撑该课程目标的教学内容,假设某门课程有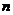 个课程目标,支撑第
个课程目标,支撑第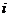 个课程目标的教学内容试卷考核总分为
个课程目标的教学内容试卷考核总分为 ,抽取的样本学生该部分的试卷考核平均分数为
,抽取的样本学生该部分的试卷考核平均分数为 ,
, 是该课程支撑第
是该课程支撑第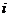 个课程目标的形成性考核的平均得分(形成性考核一般包括课堂表现、平时作业和平时测验等),支撑第
个课程目标的形成性考核的平均得分(形成性考核一般包括课堂表现、平时作业和平时测验等),支撑第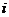 个课程目标的形成性考核总分为
个课程目标的形成性考核总分为 ,
,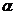 是期末试卷考核占总考核的比例,那么,第
是期末试卷考核占总考核的比例,那么,第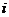 个课程目标的达成度计算公式为
个课程目标的达成度计算公式为
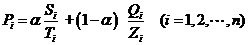 ,
,
若某个 ,即期末考核试卷中无支撑该课程目标的内容,则
,即期末考核试卷中无支撑该课程目标的内容,则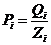 。
。
(3)课程的整体目标达成度的确定
一门课程的整体目标达成度由该课程的所有课程目标达成度的加权平均值确定。假设某门课程有 个课程目标,第
个课程目标,第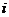 个课程目标的权重值为
个课程目标的权重值为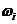 ,第
,第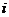 个课程目标的达成度为
个课程目标的达成度为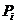
 ,那么,该门课程的整体目标达成度为
,那么,该门课程的整体目标达成度为
 .
.
(4)课程的整体目标达成度评价标准
参照best365体育官网登录入口学分制管理办法及学士学位授予条例,平均学分绩点≥2.0者才可获得理学学士学位。由于学分绩点2.0对应课程考核成绩为70分,因此,本专业课程的整体目标达成度评价标准设定为“达到0.70为评价合格”。
九、本课程各个课程目标的权重
依据第八部分中的课程目标达成度评价方法,计算得到本课程的各个课程目标的权重如下:
课程目标 |
课程目标-1 |
课程目标-2 |
课程目标-3 |
课程目标-4 |
权值 |
0.276 |
0.310 |
0.310 |
0.104 |
十、持续改进
根据学生的课堂表现、平时作业、平时测验情况及教学督导的反馈,检验学生对本课程涉及的学科素养和学会反思的达成情况,及时对教学中的不足之处进行改进,调整教学指导策略;根据学生的课堂表现、平时作业、平时测验及期末考试成绩,检验本课程所支撑的毕业要求分解指标点的达成度情况;根据本课程所支撑的毕业要求分解指标点的达成度情况,参考优秀专业经验,在本学院教学指导委员会指导下,重新修订本课程大纲,实现持续改进。
十一、推荐教材及参考书目
1.推荐教材
北京大学数学系几何与代数教研室前代数小组编,高等代数(第四版),北京:高等教育出版社,2013.
张禾瑞,郝鈵新,高等代数(第五版),北京:高等教育出版社,2007.
2.参考书目
蓝以中,高等代数简明教程(上、下),北京:北京大学出版社,2007.
丘维声编,高等代数(上、下),北京:清华大学出版社,2010.
王萼芳,石生明,高等代数辅导与习题解答(第四版),北京:高等教育出版社,2013.
姚慕生,谢启鸿,大学数学学习方法指导丛书:高等代数(第三版),上海:复旦大学出版社,2015.









