《常微分方程》课程大纲
一、课程概况
课程名称 |
常微分方程 |
课程代码 |
073CA8012A |
适用专业 |
数学与应用数学 |
开课学期 |
第3学期 |
课程性质 |
学科基础课程 |
学时/学分 |
72/4 |
课程负责人 |
向长合 |
课程组成员 |
芮伟国、杨志春、周寿明、李书平 |
预修课程 |
《数学分析》、《高等代数》、《解析几何》 |
二、课程目标
课程目标1:了解《常微分方程》的发展历史,理解《常微分方程》中的基本概念,熟练掌握《常微分方程》中的基本求解方法,加强学生的运算和解题能力。
课程目标2:掌握一阶微分方程、高阶线性微分方程和线性微分方程组的基本理论,培养学生的逻辑推理能力、抽象思维能力以及严谨的数学语言表达能力,为学习后续课程以及进一步获得更高层次的数学专业知识奠定系统的理论基础。
课程目标3:培养学生运用《常微分方程》知识的综合能力及分析和解决实际问题的能力,使学生具备一定的科学研究能力。
课程目标4:通过课前预习、课堂引导和启发、课后作业等方式,激发学生探索与求知的欲望,培养学生自主学习的能力。
三、课程目标与毕业要求的关系
1、课程目标与毕业要求的对应关系
毕业要求 |
指标点 |
课程目标 |
学会教学 |
学科素养 |
3.2掌握数学学科的基本知识、基本原理和基本技能,理解数学学科知识体系的基本思想和方法,具有良好的数学抽象、逻辑推理、数学建模、直观想象等数学学科专业能力。 |
课程目标1 课程目标2 课程目标3 |
3.3了解数学与物理和计算机等其他相关学科的联系,了解所教学科与实践应用的联系,掌握一定的数学学科相关知识。 |
课程目标2 课程目标3 |
教学能力 |
|
|
学会发展 |
学会反思 |
7.1具有主动学习新知识、掌握新技能的兴趣和意识,具有终身学习和专业发展意识,能通过不断学习和改进养成自主学习的习惯,并能进行职业生涯规划。 |
课程目标3 课程目标4 |
沟通合作 |
|
|
2、课程目标与毕业要求的矩阵关系图
名称 |
践行师德 |
学会教学 |
学会育人 |
学会发展 |
师德规范 |
教育情怀 |
学科素养 |
教学能力 |
班级管理 |
综合育人 |
学会反思 |
沟通合作 |
1-1 |
1-2 |
1-3 |
2-1 |
2-2 |
2-3 |
3-1 |
3-2 |
3-3 |
4-1 |
4-2 |
4-3 |
5-1 |
5-2 |
6-1 |
6-2 |
6-3 |
7-1 |
7-2 |
7-3 |
8-1 |
8-2 |
常微分方程 |
|
|
|
|
|
|
|
H |
H |
|
|
|
|
|
|
|
|
H |
|
|
|
|
常微分方程 |
|
|
H |
|
|
|
M |
|
课程目标1 |
|
|
|
|
|
|
|
H |
M |
|
|
|
|
|
|
|
|
M |
|
|
|
|
课程目标2 |
|
|
|
|
|
|
|
H |
M |
|
|
|
|
|
|
|
|
M |
|
|
|
|
课程目标3 |
|
|
|
|
|
|
|
M |
H |
|
|
|
|
|
|
|
|
L |
|
|
|
|
课程目标4 |
|
|
|
|
|
|
|
L |
L |
|
|
|
|
|
|
|
|
H |
|
|
|
|
四、课程教学要求与重难点
序号 |
课程内容 框架 |
教学要求 |
教学重点 |
教学难点 |
1 |
常微分方程模型及微分方程的基本概念 |
具备能够利用微分方程来建立一些简单的数学模型的能力,并在此基础上理解微分方程的一些基本概念。 |
微分方程的阶、常微分方程与偏微分方程、线性微分方程、非线性微分方程、微分方程的通解与特解、微分方程方程的初始条件与初值问题、积分曲线等基本概念。 |
微分方程数学模型的建立。 |
2 |
一阶微分方程的初等解法 |
熟练掌握变量分离方程以及可化为变量分离方程的一些方程类型的求解方法;掌握利用常数变易法求解非齐次线性微分方程的通解;掌握Bernoulli方程的求解方法;掌握恰当微分方程求解方法以及非恰当微分方程的积分因子的概念及求方法;掌握一阶隐式微分方程的四类求解方法。 |
变量分离方程、齐次方程、非齐次线性方程、Bernoulli方程、恰当方程、四种特殊情况下的一阶隐式方程的解法及一些特殊情况下积分因子的求法。 |
Bernoulli方程的求解方法、具有积分因子的非恰当方程求解方法、四种特殊情况下的一阶隐式方程的求解方法。 |
3 |
一阶微分方程的解的存在定理 |
掌握一阶微分方程的一般理论,包括解的存在唯一性定理、解的延拓概念、解对初值的连续性和可微性定理。会用皮卡的逐步迭代法求一阶微分方程的近似解并能够进行误差估计。 |
解的存在唯一性定理的理解和证明,初值问题解的存在区间及误差估计、逐次逼近解的计算。 |
存在唯一性定理的证明过程。解对初值的连续性和可微性定理。 |
4 |
高阶微分方程 |
掌握高阶线性微分方程的一般理论;掌握常系数非齐次线性方程的解法;掌握欧拉方程的解法;掌握可降阶的高阶方程的解法;理解质点的振动和第二宇宙速度等力学原理;理解微分方程的幂级数解法。 |
高阶线性微分方程初值问题的存在唯一性定理、线性相关、线性无关、Wronsky行列式的定义、高阶齐线性微分方程的叠加原理、线性相关函数组与Wronsky行列式的关系、高阶齐线性微分方程的n个线性相关解与Wronsky行列式的关系、高阶齐线性微分方程的基本解组的存在性定理、高阶齐线性微分方程的通解结构定理、高阶非齐线性方程与对应的齐线性微分方程的解的关系、高阶非齐线性方程通解结构定理及常数变易法。 |
高阶线性微分方程的一般理论、常数变易法、可降阶的高阶方程的解法。 |
5 |
线性微分方程组 |
掌握一阶线性微分方程组的解的存在唯一性定理;会将高阶线性微分方程转化成一阶线性微分方程组并进一步掌握高阶线性微分方程的解的存在唯一性定理;掌握一阶线性微分方程组的一般理论;掌握常系数一阶线性微分方程组的求解方法。 |
齐线性微分方程组的叠加原理、向量函数组线性相关、线性无关、Wronsky行列式的定义、线性相关向量函数组与Wronsky行列式的关系、齐线性微分方程组的n个线性相关解与Wronsky行列式的关系、齐线性微分方程组的基本解组的存在性定理、齐线性微分方程组的通解结构定理、解矩阵和基解矩阵的性质、非齐线性方程组与对应的齐线性微分方程组的解的关系、非齐线性方程组通解结构定理及常数变易法。 |
线性微分方程组的一般理论、常系数齐次线性微分方程组的系数矩阵的特征根有重根时,基解矩阵的求解方法。常系数非齐次线性微分方程组满足初值条件的解的求解方法。 |
五、课程教学内容、教学方式、学时分配及对课程目标的支撑情况
序号 |
课程内容框架 |
教学内容 |
教学方式 |
学时 |
支撑 课程目标 |
1 |
常微分方程模型及微分方程的基本概念 |
常微分方程模型:解决实际问题中出现的微分方程模型的建立。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
2 |
课程目标1 课程目标3 课程目标4 |
基本概念:微分方程的阶、常微分方程与偏微分方程、线性微分方程、非线性微分方程、微分方程的通解与特解、微分方程方程的初始条件与初值问题、积分曲线等基本概念。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
2 |
课程目标1 课程目标4 |
2 |
一阶微分方程的初等解法 |
变量分离方程与变量变换:变量分离方程以及可化为变量分离方程类型的方程的求解方法以及其在物理学、人口学、经济学、考古学等方面的应用。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
8 |
课程目标1 课程目标3 课程目标4 |
线性方程与常数变易法:一阶线性微分方程的常数变易法及常数变易公式、Bernoulli方程的解法。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
2 |
课程目标1 课程目标4 |
恰当方程与积分因子:方程成为恰当方程的充要条件及恰当方程的求解方法、积分因子的概念及一些特殊情况下积分因子的求法;具有积分因子的非恰当微分方程的求解方法。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
4 |
课程目标1 课程目标2 课程目标4 |
一阶隐式方程与参数表示:四种特殊情况下的一阶隐式方程的求解方法、总结有初等解法的微分方程类型及相应求解方法。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
4 |
课程目标1 课程目标2 课程目标4 |
3 |
一阶微分方程的解的存在定理 |
解的存在唯一性定理与逐步逼近法:一阶微分方程初值问题的解存在与唯一的条件、Picard逐步迭代序列的构造、存在唯一性定理的证明过程(五个命题)、近似解的求法以及解的存在区间和误差估计。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
5 |
课程目标1 课程目标2 课程目标3 课程目标4 |
解的延拓及解对初值的连续性和可微性定理:解的延拓定理。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
1 |
课程目标1 课程目标2 课程目标4 |
4 |
高阶微分方程 |
高阶线性微分方程初值问题的存在唯一性定理、线性相关、线性无关、Wronsky行列式的定义、高阶齐线性微分方程的叠加原理、线性相关函数组与Wronsky行列式的关系、高阶齐线性微分方程的n个线性相关解与Wronsky行列式的关系、高阶齐线性微分方程的基本解组的存在性定理、高阶齐线性微分方程的通解结构定理、高阶非齐线性方程与对应的齐线性微分方程的解的关系、高阶非齐线性方程通解结构定理及常数变易法。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
6 |
课程目标1 课程目标2 课程目标4 |
常系数线性方程的解法:复值函数、复指数函数及复值解的性质,包括连续性和可微性、Euler公式、高阶常系数齐次线性方程的待定指数函数法和Euler方程的解法、求解高阶非齐次线性方程类型的比较系数法及相应求解方法、(选讲)质点在有阻尼(无阻尼)状态下自由振动及强迫振动的振动规律。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
10 |
课程目标1 课程目标2 课程目标4 |
高阶方程的降阶与幂级数解法:三类可降阶的微分方程类型及相应的求解方法、(选讲)幂级数解的形式以及n阶Bessel方程解的表达式。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
6 |
课程目标1 课程目标2 课程目标4 |
5 |
线性微分方程组 |
存在唯一性定理:向量函数及矩阵函数的性质,高阶微分方程初值问题与一阶线性微分方程组初值问题的等价性、一阶线性微分方程组初值问题的存在唯一性定理的证明。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
4 |
课程目标1 课程目标2 课程目标4 |
齐线性微分方程组的叠加原理、向量函数组线性相关、线性无关、Wronsky行列式的定义、线性相关向量函数组与Wronsky行列式的关系、齐线性微分方程组的n个线性相关解与Wronsky行列式的关系、齐线性微分方程组的基本解组的存在性定理、齐线性微分方程组的通解结构定理、解矩阵和基解矩阵的性质、非齐线性方程组与对应的齐线性微分方程组的解的关系、非齐线性方程组通解结构定理及常数变易法。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
8 |
课程目标1 课程目标2 课程目标4 |
常系数线性微分方程组:矩阵指数expA及exp(At)的定义及性质、当系数矩阵A具有n个线性无关特征向量时, 基解矩阵的计算、当系数矩阵A没有n个线性无关特征向量时, 基解矩阵的计算方法(空间分解)、利用Jordan标准型以及Hamiton-Cayley定理计算基解矩阵、(可补充)利用循环列计算基解矩阵。 |
讲授、课堂讨论、课堂引导与启发下的课堂训练和课外作业布置 |
10 |
课程目标1 课程目标2 课程目标4 |
六、课程目标与考核内容
课程目标 |
考核内容 |
课程目标-1了解《常微分方程》的发展历史,理解《常微分方程》中的基本概念,熟练掌握《常微分方程》中的基本求解方法,加强学生的运算和解题能力。 |
1、微分方程的阶、常微分方程与偏微分方程、线性微分方程、非线性微分方程、微分方程的通解与特解、微分方程方程的初始条件与初值问题、积分曲线、恰当方程与积分因子、线性相关、线性无关、Wronsky行列式、矩阵指数、基解矩阵等基本概念; 2、变量分离方程、齐次方程、非齐次线性方程、Bernoulli方程、恰当方程、四种特殊情况下的一阶隐式方程的解法及一些特殊情况下积分因子的求法、高阶非齐线性方程的常数变易法、高阶常系数齐次线性方程的待定指数函数法和Euler方程的解法、求解高阶非齐次线性方程类型的比较系数法、高阶方程的降阶法、矩阵指数expA及exp(At)的计算方法、当系数矩阵A具有n个线性无关特征向量时, 基解矩阵的计算、当系数矩阵A没有n个线性无关特征向量时, 基解矩阵的计算方法(空间分解)、利用Jordan标准型以及Hamiton-Cayley定理计算基解矩阵、(可补充)利用循环列计算基解矩阵。 3、出勤、课堂表现和平时作业的完成情况; 4、平时测验成绩; 5、期末考试成绩。 |
课程目标-2掌握一阶微分方程、高阶线性微分方程和线性微分方程组的基本理论,培养学生的逻辑推理能力、抽象思维能力以及严谨的数学语言表达能力,为学习后续课程以及进一步获得更高层次的数学专业知识奠定系统的理论基础。 |
1、一阶微分方程成为恰当方程的充要条件、一阶微分方程解的存在唯一性定理、高阶线性微分方程初值问题的存在唯一性定理、线性相关、线性无关、Wronsky行列式的定义、高阶齐线性微分方程的叠加原理、线性相关函数组与Wronsky行列式的关系、高阶齐线性微分方程的n个线性相关解与Wronsky行列式的关系、高阶齐线性微分方程的基本解组的存在性定理、高阶齐线性微分方程的通解结构定理、高阶非齐线性方程与对应的齐线性微分方程的解的关系、高阶非齐线性方程通解结构定理、齐线性微分方程组的叠加原理、向量函数组线性相关、线性无关、Wronsky行列式的定义、线性相关向量函数组与Wronsky行列式的关系、齐线性微分方程组的n个线性相关解与Wronsky行列式的关系、齐线性微分方程组的基本解组的存在性定理、齐线性微分方程组的通解结构定理、解矩阵和基解矩阵的性质、非齐线性方程组与对应的齐线性微分方程组的解的关系、非齐线性方程组通解结构定理; 2、出勤、课堂表现和平时作业的完成情况。 3、平时测验成绩; 4、期末考试成绩。 |
课程目标-3培养学生运用《常微分方程》知识的综合能力及分析和解决实际问题的能力,使学生具备一定的科学研究能力。 |
1、综合本课程知识解决相关数学问题; 2、综合本课程知识分析和解决诸如物理学、人口学、经济学、考古学等方面的应用实际问题,3、出勤、课堂表现和平时作业的完成情况。 4、平时测验成绩; 5、期末考试成绩。 |
课程目标-4通过课前预习、课堂引导和启发、课后作业等方式,激发学生探索与求知的欲望,培养学生自主学习的能力。 |
1、出勤、课堂表现和平时作业的完成情况; 2、平时测验成绩。 |
七、考核方式与评价细则
课堂
表现
10%
评价标准:全勤且主动发言计100分,全勤但不主动发言计90分。在此标准下,本课程按以下细则考核课堂表现:
(1)每旷课一次扣10分;
(2)每迟到或者早退一次扣5分;
(3)上课时玩手机一次扣5分;
(4)事假一次扣5分;
(5)病假、公假、丧假不扣分。
平时
作业
20%
评价标准:将一个教学班分成三至四个小组,每次批改一个小组的作业,根据学生作业完成程度给出A(90-100分)、B(80-89分)、C(70-79分)、D(60-69分)、E(0-59分)等级,一学期一个学生大约上交四次作业,全部为A计100分。在此标准下,本课程按以下细则考核平时作业:
(1)少交一次作业扣10分;
(2)少得一个A扣5分。
平时
测验
20%
严格按照《常微分方程》平时测验试题参考答案及评分细则进行阅卷。
期末
考试
50%
严格按照《常微分方程》期末试题参考答案及评分细则进行阅卷。
综合
成绩
100%
课堂表现(10%)+平时作业(20%)+平时测验(20%)+期末考试(50%)
八、课程目标达成度评价
1、课程目标达成度评价机制
(1)评价机构
课程目标达成度评价在best365体育官网登录入口教学指导委员会的指导下进行,由课程负责人负责实施,承担该门课程的所有任课教师共同参与评价。
(2)数据来源
课程目标达成度评价采用的数据源自课程考核的成绩,课程考核成绩包含出勤成绩、课堂表现成绩、平时作业成绩、期中测试成绩(期中论文成绩或报告成绩)和期末试卷考核成绩等。
(3)评价周期
本专业课程目标达成度评价周期一般为1年。
2、课程目标达成评价方法
每门课程应有3-5个课程目标,每个课程目标对8个毕业要求分解指标点的支撑情况是不相同的,按照各个课程目标对8个毕业要求分解指标点的支撑力度,对每个课程目标赋予权重值。根据一门课程的所有课程目标都应该对该课程的整体目标达成有所贡献的原则,该课程的整体目标达成度由该课程的所有课程目标达成度的加权平均值确定。
(1)各个课程目标权重值的确定
每门课程一般有3-5个课程目标,每个课程目标对8个毕业要求的支撑力度有高(H)、中(M)、低(L)之分,为了便于操作,赋值H=3, M=2, L=1。假设某门课程有 个课程目标,第
个课程目标,第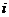 个课程目标对8个毕业要求分解指标点的支撑力度有
个课程目标对8个毕业要求分解指标点的支撑力度有 个H、
个H、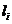 个M和
个M和 个L,那么,第
个L,那么,第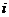 个课程目标的分值
个课程目标的分值 ,第
,第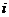 个课程目标的权重值确定为
个课程目标的权重值确定为
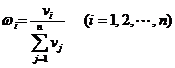 ,
,
所有课程目标的权重值之和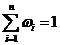 。
。
(2)各个课程目标达成度的计算
各个课程目标达成度评价采用“考核成绩分析法”,随机抽取1-2个教学班级为样本,课程考核材料包括考试、测验、作业、考勤、实验(实习、设计)报告、读书报告等。每个课程目标都有支撑该课程目标的教学内容,假设某门课程有 个课程目标,支撑第
个课程目标,支撑第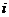 个课程目标的教学内容试卷考核总分为
个课程目标的教学内容试卷考核总分为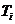 ,抽取的样本学生该部分的试卷考核平均分数为
,抽取的样本学生该部分的试卷考核平均分数为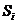 ,
, 是该课程支撑第
是该课程支撑第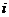 个课程目标的形成性考核的平均得分(形成性考核一般包括课堂表现、平时作业和平时测验等),支撑第
个课程目标的形成性考核的平均得分(形成性考核一般包括课堂表现、平时作业和平时测验等),支撑第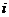 个课程目标的形成性考核总分为
个课程目标的形成性考核总分为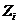 ,
,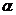 是期末试卷考核占总考核的比例,那么,第
是期末试卷考核占总考核的比例,那么,第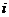 个课程目标的达成度计算公式为
个课程目标的达成度计算公式为
 ,
,
若某个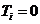 ,即期末考核试卷中无支撑该课程目标的内容,则
,即期末考核试卷中无支撑该课程目标的内容,则 。
。
(3)课程的整体目标达成度的确定
一门课程的整体目标达成度由该课程的所有课程目标达成度的加权平均值确定。假设某门课程有 个课程目标,第
个课程目标,第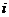 个课程目标的权重值为
个课程目标的权重值为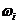 ,第
,第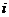 个课程目标的达成度为
个课程目标的达成度为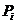
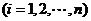 ,那么,该门课程的整体目标达成度为
,那么,该门课程的整体目标达成度为
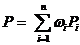 .
.
(4)课程的整体目标达成度评价标准
参照best365体育官网登录入口学分制管理办法及学士学位授予条例,平均学分绩点≥2.0者才可获得理学学士学位。由于学分绩点2.0对应课程考核成绩为70分,因此,本专业课程的整体目标达成度评价标准设定为“达到0.70为评价合格”。
九、本课程各个课程目标的权重
依据第八部分中的课程目标达成度评价方法,计算得到本课程的各个课程目标的权重如下:
课程目标 |
课程目标-1 |
课程目标-2 |
课程目标-3 |
课程目标-4 |
权值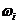 |
0.280 |
0.280 |
0.240 |
0.200 |
十、持续改进
根据学生的课堂表现、平时作业、平时测验情况及教学督导的反馈,检验学生对本课程涉及的学科素养和学会反思的达成情况,及时对教学中的不足之处进行改进,调整教学指导策略;根据学生的课堂表现、平时作业、平时测验及期末考试成绩,检验本课程所支撑的毕业要求分解指标点的达成度情况;根据本课程所支撑的毕业要求分解指标点的达成度情况,参考优秀专业经验,在本学院教学指导委员会指导下,重新修订本课程大纲,实现持续改进。
十一、推荐教材及参考书目
1.推荐教材
王高雄,周之铭,朱思铭,等. 常微分方程(第三版). 北京:高等教育出版社,2006.
张伟年, 杜正东, 徐冰. 常微分方程(第一版). 北京:高等教育出版社, 2006.
2.参考书目
丁同仁,李承治. 微分方程(第二版). 北京:高等教育出版社, 2004.
张芷芬, 丁同仁, 黄文灶,等. 微分方程定性理论. 科学出版社,1985.
张芷芬, 李承治, 郑志明,等. 向量场的分岔理论基础.高等教育出版社,1997.
张伟年. 动力系统基础. 高等教育出版社, 施普林格出版社,2001.









