best365体育官网登录入口
2021现代几何论坛
2021年12月11日 (星期六)
日程表
时间
|
报告人
|
报告题目
|
主持人
|
08:40-08:50
|
开幕式
|
中国科学院院士、发展中国家科学院院士
张伟平教授致辞
|
程新跃
|
国际系统与控制科学院院士、重庆国家应用数学中心主任
杨新民教授致辞
|
09:00-09:50
|
王长平
|
Conformally flat hypersurfaces in R41
|
张伟平
|
10:00-10:50
|
冯惠涛
|
Superconnections and an intrinsic Gauss-Bonnet-Chern formula for Finsler manifolds
|
丁青
|
11:00-11:50
|
胡泽军
|
On canonical submanifolds of the homogeneous nearly Kahler manifold 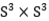
|
郑方阳
|
12:00-14:00
|
午餐
|
15:00-15:50
|
傅吉祥
|
有限个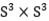 的连通和的几何 的连通和的几何
|
郑方阳
|
16:00-16:50
|
熊革
|
The Lp Minkowski problem for the electrostatic ℘ -capacity
|
周家足
|
17:00-17:50
|
许洪伟
|
New developments in mean curvature flow of arbitrary codimension inspired by Yau rigidity theory
|
东瑜昕
|
17:50-18:00
|
闭幕式
|
|
程新跃
|
18:30-21:00
|
晚餐
|
报告地点:best365体育官网登录入口221学术报告厅
腾讯ID:928 763 654 密码:123456
主办单位:版权所有:best365体育官网登录入口 - 365wm完美体育官网
best365体育官网登录入口“2021现代几何论坛”系列报告1
报告题目: Conformally flat hypersurfaces in R41
报 告 人:王长平 教授 (福建师范大学)
摘要:In this talk, we will give a complete classification of generic conformally flat Lorentzian hypersurfaces in R41.
时间:2021年12月11日 9:00 – 9:50
地点:线上:腾讯会议(ID: 928 763 654; 密码:123456)
线下:best365体育官网登录入口221学术报告厅
报告人简介:王长平,教授,教育部“长江学者奖励计划特聘教授”,现任福建师范大学校长,九三学社福建省委员会副主任委员。先后师从著名数学家姜伯驹院士及数学大师陈省身教授;1992年9月-1995年7月在柏林工业大学师从著名数学家Udo Simon教授,获博士学位。先后担任北京大学数学学院院长、北京数学会理事长、中国数学会第十届理事会秘书长。2002年获得教育部科技进步奖二等奖,同年获批国家杰出青年基金;2009年获批教育部长江学者特聘教授;2008年获评北京市师德标兵荣誉称号;2009年获得国家级教学成果二等奖,2014年获教育部自然科学奖一等奖。
王长平教授建立了中心仿射微分几何的不变量理论的基本框架,给出了中心仿射度量面积的第一和第二变分公式、共形微分几何子流形理论的基本框架,给出了高维子流形所使用的不变量系统并引导了一系列的研究工作,构建了Laguerre微分几何超曲面理论的基本框架,给出了完全的不变量系统,为Lie球几何的子几何-Laguerre微分几何做出了重要贡献。
best365体育官网登录入口“2021现代几何论坛”系列报告2
报告题目:Superconnections and An Intrinsic Gauss-Bonnet-Chern Formula for Finsler Manifolds
报 告 人:冯惠涛 教授 (南开大学陈省身数学研究所)
摘要:In this talk, we will represent the Euler class of an even dimensional closed and oriented manifold by the geometric data of a Finsler metric on this manifold. In this way, we obtain an intrinsic GBC-formula for Finsler Manifolds. Furthermore, by a geometric localization process, we get a new proof of Lichnerowicz's GBC-formula related to a transversal vector field.
时间:2021年12月11日 10:00 – 10:50
地点:线上:腾讯会议(ID: 928 763 654; 密码:123456)
线下:best365体育官网登录入口221学术报告厅
报告人简介:冯惠涛,南开大学陈省身数学研究所副所长、教授、博士生导师,研究领域为整体微分几何,主要研究方向为Atiyah-Singer 指标理论及其应用、黎曼-芬斯勒几何。已先后主持国家自然科学基金重点项目及面上项目多项。
best365体育官网登录入口“2021现代几何论坛”系列报告3
报告题目:On canonical submanifolds of the homogeneous nearly Kahler manifold 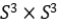
报 告 人:胡泽军 教授 (郑州大学)
摘要:In this lecture, I will talk about our researches on submanifolds
of the homogeneous nearly Kahler manifold 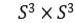 . Our results are concentrated on the classification of the canonical hypersurfaces and Lagrangian submanifolds.
. Our results are concentrated on the classification of the canonical hypersurfaces and Lagrangian submanifolds.
时间:2021年12月11日 11:00 – 11:50
地点:线上:腾讯会议(ID: 928 763 654; 密码:123456)
线下:best365体育官网登录入口221学术报告厅
报告人简介:胡泽军,郑州大学数学与统计学院博士生导师、二级教授、中国数学会理事、国际数学期刊《Journal of Geometry》和《JP Journal of Geometry and Topology》编委。已先后主持河南省杰出青年科学基金和国家自然科学基金面上项目五项。研究方向为微分几何,研究领域涉及子流形的几何与拓扑、共形微分几何、仿射微分几何。在等仿射超曲面和中心仿射超曲面研究中做出了较为系统深入的重要工作。
best365体育官网登录入口“2021现代几何论坛”系列报告4
报告题目:有限个S3XS3的连通和的几何
报 告 人:傅吉祥 教授 (复旦大学)
摘要:我们将介绍这类流形上复结构与平衡度量的构造以及它们的几何应用。
时间:2021年12月11日 15:00 – 15:50
地点:线上:腾讯会议(ID: 928 763 654; 密码:123456)
线下:best365体育官网登录入口221学术报告厅
报告人简介:傅吉祥,男,复旦大学best365体育官网登录入口教授,复旦大学数学研究所所长,国家杰出青年科学基金获得者。 2015年获第十五届中国数学会陈省身奖。
傅吉祥教授在复几何,特别在非凯勒复几何的研究领域做出了一系列国际领先的具有原创性的研究成果。他与丘成桐教授合作,首次在非Kahler流形上解出了Strominger方程组,解决了这方面长达20年的悬而未决的问题,该问题的解决被认为是这一重要方向的一个突破。这些成果引起了国际学术界的广泛关注和引发了一大批后续研究,促进了非凯勒复几何的发展。
因研究非Kahler卡-丘空间的工作,2010年应邀在国际数学家大会上作45分钟报告;获晨兴数学奖银奖。
best365体育官网登录入口“2021现代几何论坛”系列报告5
报告题目:The Lp Minkowski Problem for the Electrostatic ℘-Capacity
报 告 人:熊革 教授 (同济大学)
摘要:Existence and uniqueness of the solution to the Lp Minkowski problem for the electrostatic ℘-capacity are proved when p > 1 and 1 < ℘ < n. These results are nonlinear extensions of the solution to the Lp Minkowski problem for ℘-capacity when p = 1 and 1 < ℘ < n by Colesanti et al. and Akman et al., and the classical solution to the Minkowski problem for electrostatic capacity when p = 1 and ℘ = 2 by Jerison.
时间:2021年12月11日 16:00 – 16:50
地点:线上:腾讯会议(ID: 928 763 654; 密码:123456)
线下:best365体育官网登录入口221学术报告厅
报告人简介:熊革,同济大学教授,博士生导师。2003年毕业于武汉大学数学学院,师从著名几何学家任德麟教授,获得理学博士学位。主要研究凸体几何。
熊革教授解决了Lp静电容量的Minkowski 问题;提出并证明了“Lp transference principle”,对Lp Brunn-Minkowski型不等式进行了统一处理; 定义了凸体的投影平均椭球,建立了仿射均质积分的严格等周不等式;解决了凸体几何中的几个公开问题,包括锥体积泛函仿射极值的Lutwak-Yang-Zhang公开问题的2, 3维情形;由截面确定凸体的Baker-Larman公开问题的2维情形;完全解决了G. Zhangbest365体育官网登录入口关于凸体的John 椭球与对偶惯性椭球的一致性问题。已在国际重要数学期刊如Journal of Differential Geometry, Advances in Mathematics, Journal of Functional Analysis, Communications in Analysis and Geometry, Israel Journal of Mathematics等发表论文近30篇;多个研究成果被写入凸体几何的经典教材《Geometric Tomography》和《Convex Bodies: the Brunn-Minkowski theory》中。
best365体育官网登录入口“2021现代几何论坛”系列报告6
报告题目:New Developments in Mean Curvature Flow of Arbitrary Codimension Inspired by Yau Rigidity Theory
报 告 人:许洪伟教授 (浙江大学)
摘要:In this talk, we will focus on the mean curvature flow theory with sphere theorems, and discuss the recent developments on the convergence theorems for the mean curvature flow of arbitrary codimension inspired by the Yau rigidity theory of submanifolds. Several new differentiable sphere theorems for submanifolds are obtained as consequences of the convergence theorems for the mean curvature flow. It should be emphasized that our convergence theorem in the hyperbolic space is an optimal convergence theorem for the mean curvature flow of arbitrary codimension, which implies the first optimal differentiable sphere theorem for submanifolds with positive Ricci curvature. Finally, we present a list of unsolved problems in this area.
时间:2021年12月11日 17:00 – 17:50
地点:线上:腾讯会议(ID: 928 763 654; 密码:123456)
线下:best365体育官网登录入口221学术报告厅
报告人简介:许洪伟,浙江大学教授,博士生导师,浙江大学数学中心副主任。2016年8月应邀在第7届世界华人数学家大会上作一小时大会报告,是浙江省第一位获此荣誉的全职数学家。曾担任美国著名SCI数学期刊《Pure and Applied Math. Quarterly》执行主编(2004.7-2019.6)、丘成桐大学生数学竞赛组委会副主席。主持承担国家自然科学基金重点项目《子流形与曲率流》,先后九次获得国家自然科学基金科研项目资助。获教育部自然科学奖二等奖、教育部科技进步奖三等奖、浙江省教委科技进步奖一等奖,并获世界华人数学家联盟最佳论文奖(若琳奖)等奖励。入选国家教育部跨世纪优秀人才(2000)、浙江省151人才工程第一层次(1998)。